Maths for metallurgy. Linear programming and furnace metallic charge optimizations
-
Tags
Linear programming is a rather new optimization technique, whose origin can be found in the development of tools for military decision making during World War II. It is a set of procedures that allow maximizing or minimizing a target function, which is subjected to a set of linear restrictions.
The systematization of these procedures and the demonstration of their validity in a given frame of rules and axioms are owed to the mathematician George B. Dantzig. In 1963, Dantzig published with RAND Corporation (property of the United States Air Forces) an extensive handbook on linear programming under the title “Linear Programming and Extensions”.
In this first linear programming text it was possible to identify one of the early applications of this discipline in the field of metallurgy: the mixing problems associated to the furnace metallic charge.
In this blog text I will show a variation of the example 3-4 from Dantzig’s handbook to explain the value and usefulness of this discipline.
The problem to be solved is related to optimizing the cost of the raw materials used by a foundry to achieve an alloy with a chemical composition of 30% Ni, 30% Cr and 40% Fe.
Different raw material options will be available on the market, each with its own composition and price. The following composition and price table will be taken as an example of sourcing from suppliers A to I.
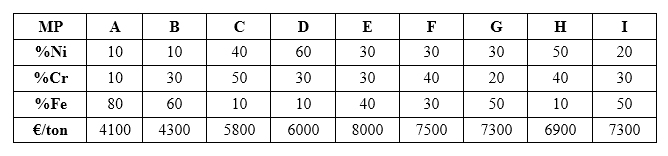
Composition and price table will be taken as an example of sourcing from suppliers A to I
The foundry can buy straight from the supplier E, whose raw material corresponds to the target alloy at a price of 8000€/ton and avoid the harassment of adjusting the metal composition in the melting furnace. On a trial and error basis though, it can be identified that mixing a part of A and B with two parts of H, the same composition is achieved at a cost of 5550€/ton. But performing some further calculations, it can be found that this result can be improved, since mixing a part of A, B, C and D, the target alloy can be manufactured at 5050€/ton. It would be possible to find the optimal mix, the most competitive, just by calculating the cost of all the possible supplier source combinations and taking the cheapest.
Nevertheless, this would mean performing a huge number of calculations to sweep all the range of possible mixes leading to 30% Ni, 30% Cr and 40% Fe.
Linear Programming takes the lead at this point, since it allows identifying the optimal mix with the minimum number of steps possible. It is only necessary to define the optimization function and the set of restrictions to be satisfied, and apply the Simplex method developed by Dantzig.
Since the application of the Simplex method goes beyond the scope of this Blog, only how the problem definition is done will be explained below.
In order to draw the equations describing the optimization problem, the following variables will be considered:
a = amount of supply “A” employed to manufacture one ton of the target alloy.
b = amount of supply “B” employed to manufacture one ton of the target alloy.
c = amount of supply “C” employed to manufacture one ton of the target alloy.
d = amount of supply “D” employed to manufacture one ton of the target alloy.
e = amount of supply “E” employed to manufacture one ton of the target alloy.
f = amount of supply “F” employed to manufacture one ton of the target alloy.
g = amount of supply “G” employed to manufacture one ton of the target alloy.
h = amount of supply “H” employed to manufacture one ton of the target alloy.
i = amount of supply “I” employed to manufacture one ton of the target alloy.
With this nomenclature, the target optimization function “z” must be:
4100a+4300b+5800c+600d+8000e+7500f+7300g+6900h+7300i = z (1)
which represents the price of each tone resulting from the mix. The target is thus minimizing “z”.
The restrictions are given by the obligation of satisfying a 30% of Ni, a 30% of Cr and a 40% of Fe in the melting furnace and can thus be expressed in terms of three equations:
10a+10b+40c+60d+30e+30f+30g+50h+20i=30 (2)
10a+30b+50c+30d+30e+40f+20g+40h+30i=30 (3)
80a+60b+10c+10d+40e+30f+50g+10h+50i=40 (4)
Two further implicit restrictions are recommended to be made explicit:
- It can’t be bought a negative amount of raw material:
a≥0; b≥0; c≥0; d≥0; e≥0; f≥0; g≥0; h≥0; i≥0 (5)
- The complete mix must reach 100% of the furnace load:
a+b+c+d+e+f+g+h+i=1 (6)
Applying the Simplex method to the system (1) (2) (3) (4) (5) (6) leads to an optimal solution with a cost of 4980 €/ton, which is made of 60% B and 40% D, and it can be assured that a cheaper option can’t be found.
Hoping this example has waken up your curiosity about the different optimization techniques that Ik4-Azterlan uses to reinforce the competitiveness of the metallurgical sector, we bid you farewell until our next post on maths for metallurgy.


